电力系统混沌振荡的自适应最优控制

电力系统在周期性负荷扰动的作用下会发生混沌振荡，甚至由此而失去稳定。为抑制这种情况下的混沌振荡，保证电力系统运行的稳定性，利用自适应最优控制方法设计了在周期性负荷扰动幅值不确定以及系统参数不确定情况下的混沌振荡控制器；并利用Lyapunov稳定性理论证明了受扰的、未精确建模的电力系统在该控制器作用下可以保持渐近稳定。因此，当电力系统所受到的周期性负荷扰动的幅值不确定且引起电力系统混沌振荡甚至失去稳定时，自适应最优控制器可以使电力系统获得渐近稳定，即能回到初始平衡点上。数值仿真也表明了该控制器的控制效果。
　　关键词：电力系统；混沌控制；渐近稳定；自适应

AdapTIve and OpTImal ChaoTIc oscillaTIon control of electric power system 


WANG Bao-hua1，2 ZHANG Qiang2 YANG Cheng-wu1　YANG Wei1

（1． School of Power Engineering，Nanjing University of Science 
and Technology，Nanjing 210094，China；
2．Department of Electric Power Engineering，Nanjing Institute of
 Technology，Nanjing 210013，China）

　　Abstract：The electric power system is likely to emerge chaotic oscillation or instability under stronger periodic load perturbation．Adaptive and optimal controller has been designed to restrain chaotic oscillation when the magnitude of the periodic load perturbation and the model of the electric system is uncertain．Lyapunov stability theory is used to prove this control method enable the electric system asymptotical stability. The performance of the controller has been evaluated by numerical simulation．It is concluded that such a controller can drive chaotic or unstable trajectory of power system under stronger periodic load perturbation to the initial position，i.e.，the controller can restrain chaotic oscillation and make power system obtain asymptotical stability．
　　Key words：electric power system；chaos control；asymptotical stability；adaptive

1 引言
　　电力系统作为一个典型的非线性系统，在周期性负荷扰动作用下，当周期性负荷的幅值满足一定条件时，就会发生混沌振荡^[1-3]，甚至会使电力系统失去稳定性。因此，为保证电力系统在周期性负荷扰动的作用下仍然能稳定运行，就必须消除混沌振荡现象。由于非线性反馈控制方法能够补偿系统模型的非线性，因而能够抑制混沌，这已经在许多控制系统中得到应用^[4-5]，同时非线性反馈控制还可以实现电力系统的稳定控制^[6]，因此可以利用非线性反馈控制来消除混沌，稳定系统。然而该方法要求系统必须精确建模，否则控制器无法对系统的非线性进行补偿，另外即使控制器对系统的非线性进行了补偿，在控制器作用下系统不会发生混沌振荡，但是由于周期性负荷扰动仍然存在，系统就不可能回到初始平衡点，而是在某一个稳定的周期轨道上运行^[9]。变量反馈控制法^[7]通过调节反馈系数来减小系统非线性项的影响，抑制混沌，使系统进入混沌吸引子中固有的不稳定周期轨道上，而且该方法要求首先确定混沌吸引子中的不稳定周期轨道。而对电力系统而言，我们希望其受扰后能够在控制器的作用下回到初始平衡点或者新的平衡点上，因此要寻求新的控制方法，使得系统不论受到多大幅值的周期扰动，无论系统的模型是否精确，在控制器的作用下均能回到初始或新的平衡点上，这就需要控制器能够估计周期性扰动的幅值。本文利用非线性最优控制方法与自适应控制相结合，设计了自适应最优控制器，并利用Lyapunov稳定性理论证明了受控的闭环系统能够保持渐近稳定，同时利用数值仿真，校验了该控制器的控制效果以及对周期性负荷扰动幅值的逼近情况，理论和仿真都说明了控制器的有效性。

2 简单电力系统在周期性负荷扰动下的动力学行为
　　简单互联电力系统接线图^[6]如图1所示，其中：1为系统1的等值发电机；2为系统2的等值发电机；3为系统1的等值主变压器；4为系统2的等值主变压器；5为负荷；6 为断路器；7为系统联络线。

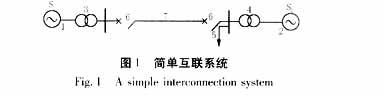
　　具有周期性负荷扰动的简单电力系统数学模型如下^[6]：
 
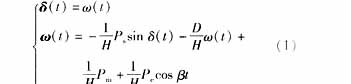
　　　　　　 　（1）
式中：δ(t) 为发电机转子运行角：w(t)为发电机相对转速；p_m和p_s分别为发电机机械功率和电磁功率；H为等值转动惯量；D为等值阻尼系数；P_e为扰动功率幅值；β为扰动功率频率。
 
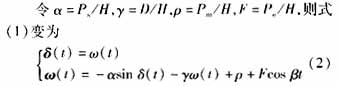
    当假设 a、γ、ρ不变即发电机的电磁功率、系统的阻尼和机械功率不变，而F变化时，上述系统变成了一个含参数F的非线性系统，当F不同即周期性负荷扰动的幅值不同时，系统呈现出不同的状态。若系统无周期性负荷扰动，则系统运行于稳定的平衡点；文献[2]详细说明了F变化时，系统的运行状态，系统可能运行于稳定的周期轨道，也可能运行于包含有许多不稳定周期轨道的混沌状态；甚至失去稳定^[8]。

3 电力系统混沌振荡的自适应最优控制
3.1 非线性最优控制器设计
　　假设系统为精确建模，系统的等值阻尼系数D，发电机的机械功率P_m以及扰动功率幅值P_e已知，也就是说γ、ρ和F已知。受控的闭环系统如下式所示。
　　
　　对该系统采用二次型最优控制方法，使
　　
式中，Q、R分别对应于状态量的权矩阵和控制量的权系数。
 
    如果系统为精确建模，且干扰的周期性负荷的幅值已知，由控制器（6）与原系统的构成的闭环系统可知，控制器将补偿系统的非线性和外部干扰，并增加了系统的阻尼，因而将抑制混沌，保证系统的渐近稳定。
3.2 自适应最优控制器设计
    由于系统的不精确建模，假设系统中等值阻尼系数D、发电机机械功率P_m、扰动功率幅值P_e等一些参数不确定，即γ、ρ和F不确定，则最优控制器中γ、ρ和F这些参数由自适应控制律来实现。同时设由最优控制律得到的最优反馈增益系数K₁=K₂=-1,并将△δ(t)=δ(t)

式中K₃,K_4,K₅均为大于零的自适应控制系数。
　　 为证明闭环系统在控制器（7）作用下能保持渐近稳定，构造如下的Lyapunov函数：
　　
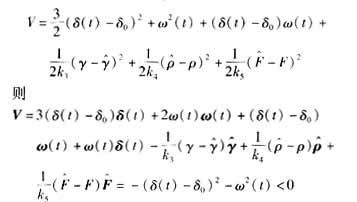
    于是，闭环系统（3）在控制器（7）作用下可以保持渐近稳定，即当电力系统受扰进入混沌状态甚至失去稳定时，其也能在控制器作用下回到初始平衡点。 

4 数值仿真分析
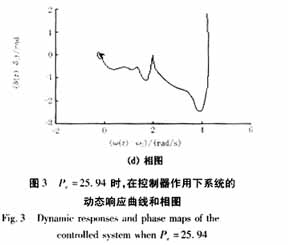
    式（1）中的参数分别取为：H=100，P_s=100，D=2，P_m=20，β=1，即a=1，γ=0.02，ρ=0.2。由文献[8]知，当P_e=25.93（F=P_e/H=0.2593），系统处于混沌状态，如图2（a）（b）的前100s所示；当P_e=25.94（F=0.2594)时，系统不仅处于混沌状态，而且在t=137s时已经失去稳定，如图3（a）、（b）的137s所示。

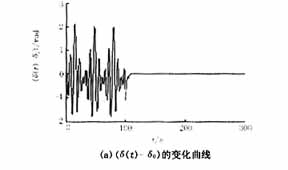
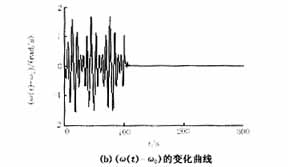
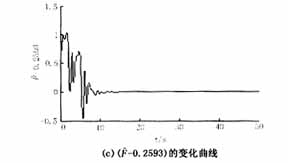
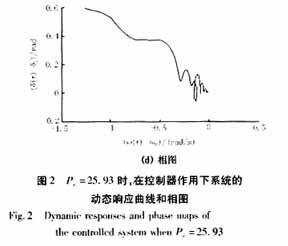
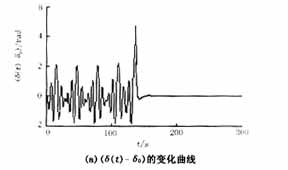
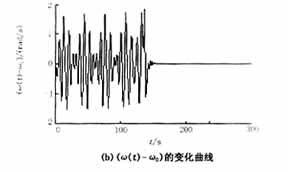
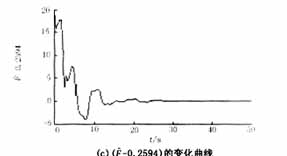
　　现针对这两种情况，考虑式（7）所示的控制器的作用。当P_e=25.93（F=P_e/H＝0.2593)，系统处于混沌状态运行100s后，投入控制器，受控系统的动态响应以及相图（δ（t)-δ₀)与(w(t)-w₀)关系曲线）如图2所示。由图2可见，在控制器的作用下，系统的混沌振荡得到了迅速的抑制，而且系统回到了初始平衡点，受控系统能够迅速的辨识周期性扰动的幅值，为清楚显示受控系统对参数的辨识能力，图2（c）中只给出了加入控制器后50s以内，F-0.2593的变化情况。
    当P_e=25.94（F=P_e/H＝0.2594)，系统失去稳定之前（t=137s时）投入控制器，受控系统的动态响应以及相图如图3所示。由图3可见，在控制器的作用下，系统迅速地进入稳定状态，而且回到了初始平衡点，受控系统也能够迅速的辨识周期性扰动的幅值。

4 结论
    由于自适应最优控制方法能够辨识系统所受周期性扰动的幅值，因此在该控制器的作用下，无论周期性负荷扰动的幅值是否已知，系统均能够回到初始平衡点，维持电力系统的稳定性，同时在自适应最优控制器的设计中假定系统是未精确建模的，因此该控制方法对系统模型的精确性没有提出很高要求，比其它的非线性反馈方法具有优越性，也可以应用在电力系统其它控制器的设计中。