为了缓解能源和环境面临的危机，在全世界范围内电动汽车得到了快速发展。锂离子电池也因高比能量和长寿命等优势而被广泛地用作车载储能载体。让电池在合适的条件下工作对充分发挥电动汽车性能意义重大。

作为电化学系统的重要特征参数，阻抗一直以来被认为是最强大电化学分析工具之一。电池的阻抗反映了带电粒子在电池内部移动所受到的阻力。利用阻抗可以更加全面地掌握电池的状态，进而为电池管理提供支持。

【工作简介】

同济大学魏学哲和戴海峰课题组在国际交通电动化杂志eTransportation上发表了关于电池阻抗的综述性文章(A Review of Modeling, Acquisition, and Application of Lithium-ion Battery Impedance for Onboard Battery Management)。文章面向车用电池管理，系统性综述了锂离子电池阻抗的建模、获取和应用三方面的研究进展和存在的问题。

【内容详情】

阻抗的相关研究可以追溯到19世纪。在过去的几个世纪中有大量的研究被报道，同时也有一些综述性的文章被发表(Huet 1998，Rodrigues et al. 2000，Macdonald 2006，Osaka et al. 2015，Nara et al. 2020)。这些综述文章大多是对电化学阻抗分析方法本身的进展进行了论述。随着电动汽车的发展，先进电池管理系统的需求越来越强，我们需要重新审视这一有力工具在车载应用上的可能性。现有的研究缺乏对阻抗方法在电池管理系统中的适用性以及可能存在的问题分析和讨论。

为此，本文面向车载应用场景，系统性地综述了阻抗的建模、获取和应用三个方面的研究进展(图1)，并对各方面面临的挑战进行分析和总结，以期为学者和工程师提供参考。

图1 本文的主要内容结构

2 阻抗的原理

2.1 定义

阻抗是线性两端口网络的重要特征。作为一个强非线性和时变性的系统，电池的阻抗需要在满足因果性、稳定性和线性条件下进行获取(Macdonald 2006)，否则得到的阻抗难以解析或失去物理意义。因此，通常情况下是在电池充分静置后，对正负极施加无偏置的弱扰动(如施加的扰动电压或响应电压在10mV左右)来获取阻抗，如图2。施加的可以是电流扰动，也可是电压扰动。但考虑电池阻抗非常小，为了避免过流通常使用电流扰动。扰动的波形没有限制。以正弦扰动为例，电池的响应电压为u=Usin(ωt+φu)，电流为i=Isin(ωt+φi)。则电池阻抗计算式如下

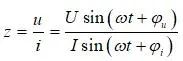
阻抗模值为

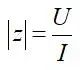
阻抗角为

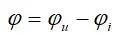
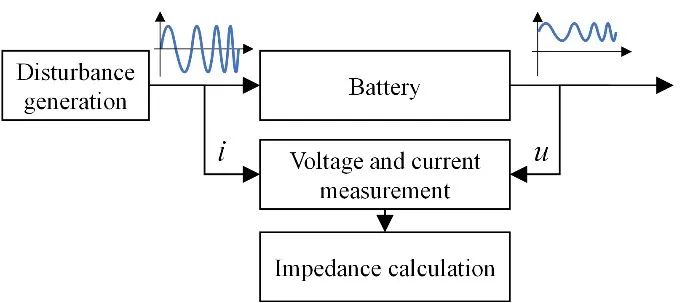
图2 电池阻抗的获取原理(电流扰动为例)

除了使用模和相角表达阻抗，也可将阻抗写成实部Z’和虚部Z’’的组合，如下式

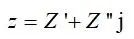
将不同频率下的阻抗实部作为横坐标，负虚部作为纵坐标可以得到电池的阻抗谱(Electrochemical Impedance Spectroscopy，EIS)。如图3为典型的电池EIS。在低频区域是一个与实轴近似45°的直线，在高频和中高频区域是两段圆弧，在超高频区域为实轴下方的曲线。当然，不是所有的电池都呈现如此特征，EIS会随电池内部过程特性和所处状态发生变化。

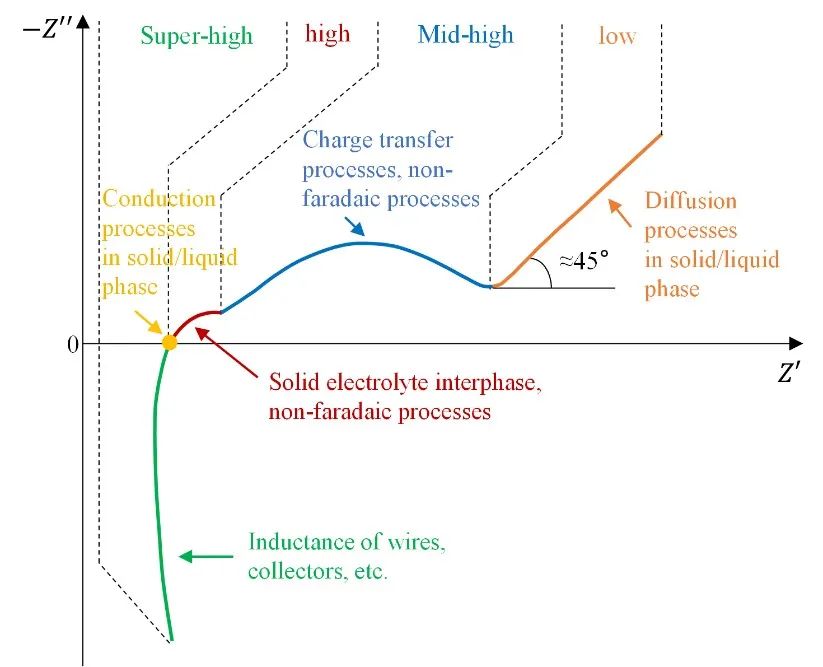
图3 典型的阻抗谱及其与电极过程对应关系

2.2 内部原理

锂离子电池是一个非常复杂的电化学系统，包含了很多电化学和物理过程，主要有固液相扩散过程、固液相电导过程以及界面过程(Doyle and Newman 1995)。包括锂离子在内的带电粒子参与到这些过程中。这些过程的时间常数不同，因此在阻抗谱上主导不同频率区间的阻抗(Munichandraiah et al. 1998)。在低频区域由最慢的离子扩散过程主导，中高频阻抗由离子嵌入的电化学反应过程主导，在高频区域主要由SEI阻抗主导，固液相的电荷转移决定了欧姆电阻大小，在超高频则是由导线、集流体等寄生电感主导。EIS与不同过程之间的对应关系使得其能够表征不同过程特性，EIS也因此具有丰富的信息内涵。

2.3 与内阻的区别

作为电池的另一个重要特征参数，内阻(包括欧姆内阻Rohm、极化内阻Rpol和直流内阻RDC)也经常在测试中被测量。它们的定义如下式和图4(FreedomCAR Battery Test Manual For Power-Assist Hybrid Electric Vehicles 2003)。很明显内阻与阻抗的定义是不一样的，是两种不同的测试方法。

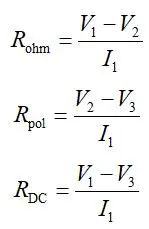
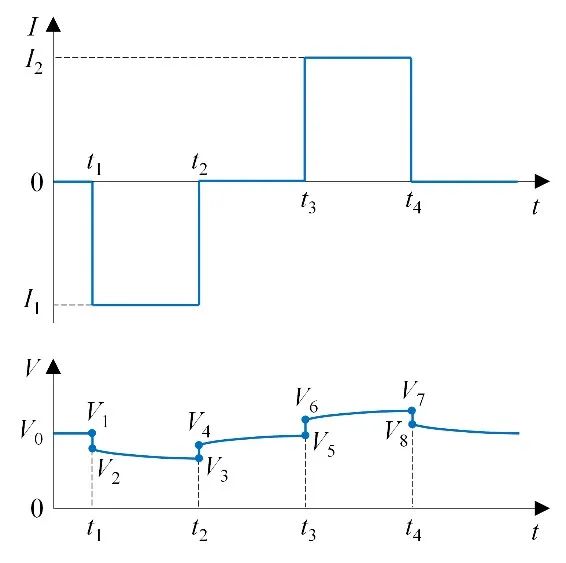
图4 用于内阻测试的电压和电流波形

阻抗是通过频域分析得到，而内阻仅依靠波形中的几个特征点来计算。从内部原理来说，不同频率的阻抗与电池内部具有不同时间常数的过程对应，是一种更加精细的过程研究方法。内阻反映了电流持续加载过程中的端电压变化。内阻无法清楚地区分内部不同过程，更适于用来描述电池的功率特性。因此，阻抗在机理相关研究中被广泛采用而形成了系统的方法论。

3 阻抗的模型

3.1 电化学阻抗模型

(1)电化学模型。以多孔电极理论为基础，简化后的P2D模型和SPM模型等被广泛用来描述电池内部的主要物理化学过程(图5)。在P2D模型中，正负极固相颗粒被等效为球形颗粒，且在电极厚度方向和颗粒半径方向包含了主要的固液相及其界面的电极过程，可以准确地对电池特性进行仿真。相比于P2D模型，SP模型更加简单，正负极被等效为一个球形颗粒，它往往忽略电池固液相传导和液相扩散过程。被忽略的过程对电势的影响采用集总参数的电阻来描述。

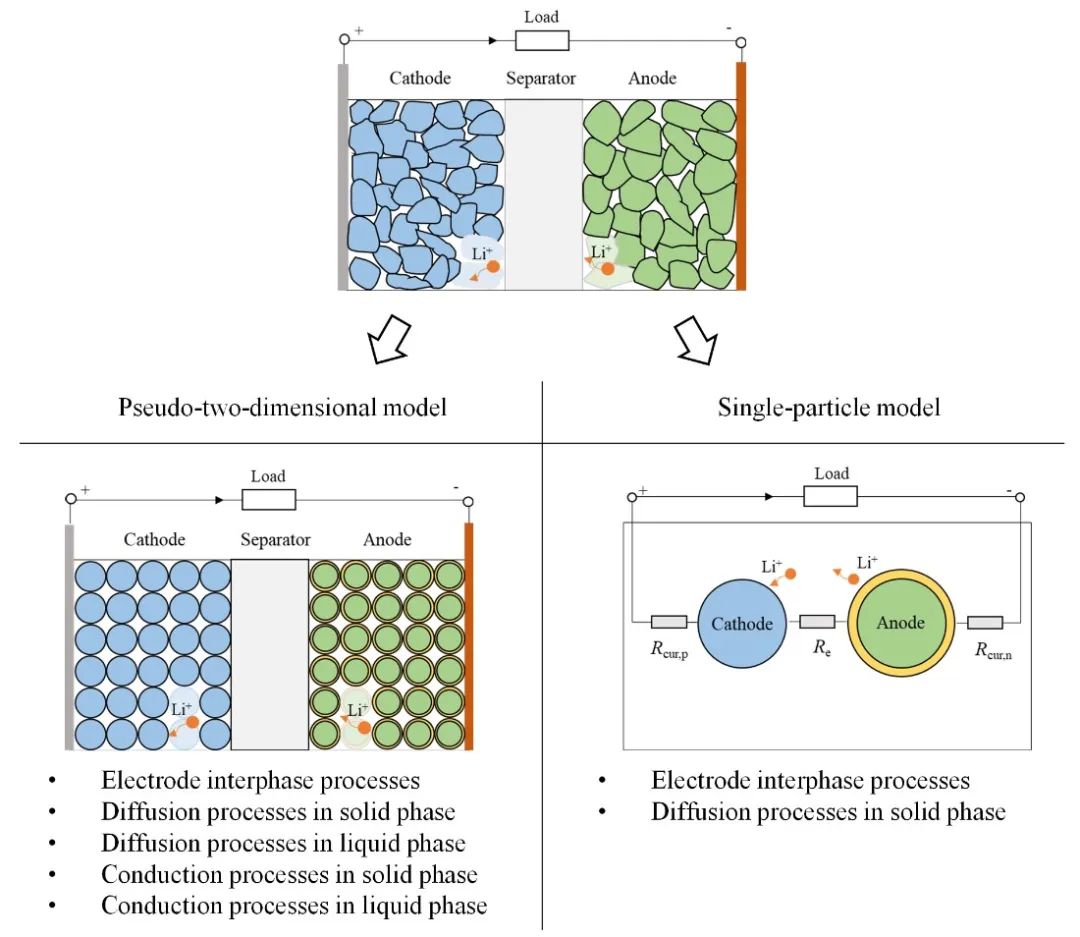
图5 锂离子电池P2D模型和SPM模型

(2)电化学阻抗模型。电化学阻抗模型可以直接从电池的电化学模型得到。由于电化学阻抗多是在很小激励下测量，描述小倍率充放电特性的SP模型被很多文献报道进行阻抗解析式的推导(Meyers et al. 2000，Li et al. 2014，Sikha et al. 2007)。SP模型耦合过程少，阻抗解析表达式容易建立。对于更为普适性和复杂的P2D模型则更多地是通过仿真得到阻抗，往往会有一些更贴近机理的过程，如DL模型(Xiao et al. 2015)和团聚物模型(Huang et al. 2014)被加入到基于P2D模型的阻抗仿真中。总之，电化学阻抗模型可以耦合电池温度、荷电状态、老化状态等变化对电池电极参数的影响规律，从而可以研究不同状态下的阻抗。

(3)非法拉第过程。通常情况下，电极界面上除了进行锂离子的嵌入脱出反应，还有等效电容的充放电过程，属于非法拉第过程，主要包括SEI膜电容和DL电容。这也是EIS在中高频区域呈现近似圆弧的原因，对界面上的膜电容模型的描述会影响此区域的阻抗描述的准确性。文献也报道了很多的膜电容等效形式(图6)。图6a只考虑DL的影响，适于描述阻抗中的一个圆弧的情况(Dokko et al. 2001)。文献认为当SEI厚度小时，可以采用图6b进行描述(Huang et al. 2014)，否则就用图6c进行(Meyers et al. 2000)。应该看到，除了从内部机理进行选择外，这其实是一种模型精度和复杂度之间的权衡。

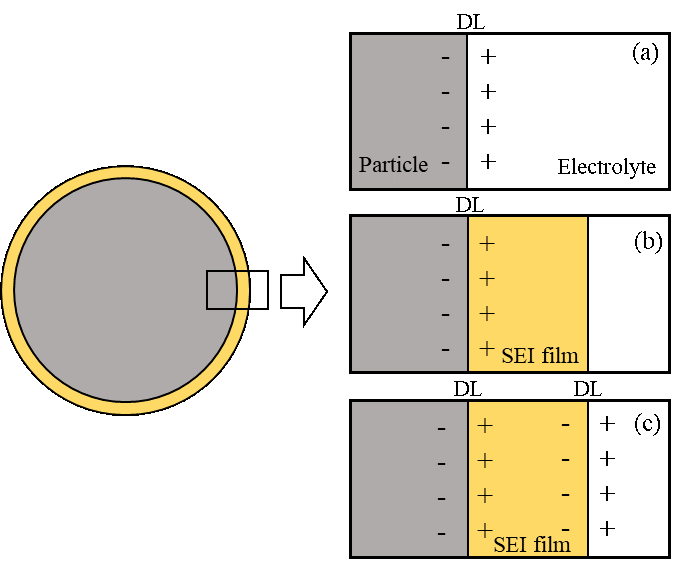
图6 不同电极界面膜电容的等效形式

3.2 等效电路模型

(1)等效元件。等效电路模型采用阻容元件、常相角元件等的组合来得到电池的宽频阻抗。这些元件一般和电池内部的电极过程对应，用来等效此部分的阻抗。膜的等效电容一般采用理想电容或更多的是考虑多孔电极弥散效应的常相角元件(CPE)进行描述。文献也报道了两种CPE的定义方法(Pauliukaite et al. 2010)。描述扩散过程的韦伯元件也根据机理过程的边界条件有三种不同的形式。

(2)等效电路模型。Ershler和Randles是最早使用等效电路模型的学者(Macdonald 2006)。到目前为止，非常多的电池等效电路模型被提出来描述电池阻抗。等效电路模型相比于电化学阻抗模型更为简单，更适于面向控制的应用。但是由于物理意义欠缺，元件是等效的，致使模型的准确性和普适性上存在不足。

(3)等效电路模型选择。文献报道了大量的等效电路模型，选择合适的等效电路模型来解析得到电池阻抗非常重要。不同的等效元件具有明显的阻抗特征，因此选择何种等效元件是容易的。关键是对于R-C或者R-CPE并联环节数量的确定，这也是文献报道的ECM的主要区别之一。不同时间常数的环节被认为与电池内部不同过程是对应的。DRT分析方法可以通过判断阻抗谱中的时间常数分布来确定选择的并联环节个数，从而帮助确定用于分析阻抗的等效电路模型(Boukamp 2015，Zhang et al. 2015，Li et al. 2019)。

4 阻抗的获取

4.1 估计阻抗

通过利用动态工况下估计等效电路模型参数可以获取电池的阻抗。因为电池的非线性，很多研究聚焦于电压和电流的非线性关系上。同时，为了得到宽频阻抗，宽频范围内的辨识方法也被研究和报道。

(1)非线性表征。在电池的SOC、SOH等估计上，由阻容元件得到的整数阶等效电路模型是常采用的。但是，大量的研究发现整数阶的等效电路模型难以精确地描述电池电压和电流特性，尤其是在频域内。例如，此类模型很难描述在阻抗谱近似于直线的低频扩散阻抗。而且由于弥散效应，理想的R-C环节也往往很好的描述中高频区域的阻抗特征。一些研究采用很多个RC并联环节来描述这些特性(Hu et al. 2012，Westerhoff et al. 2016)。但是，这增加了模型复杂度，同时也待辨识参数的数量，为参数辨识带来困难。近些年，很多学者采用分数阶等效电路模型来估计阻抗(Yuan et al. 2013，Alavi et al. 2015，Guha et al. 2018)。这类模型的关键是利用分数阶的CPE元件来描述原本需要很多R-C环节才能描述的阻抗特性。分数阶模型与整数阶不同，需要采用特殊的方法将其转换到时域。Riemann–Liouville、Grünwald–Letnikov和Caputo都是常采用的算子(Monje et al. 2010)。由于电池阻抗的时变性和非线性，分数阶模型参数并不是一成不变。特别是分数阶阶次随工况和状态的改变会导致从分数阶转换的时域模型结构的变化，这也是分数阶在复杂工况应用下的一大挑战。

(2)宽带宽辨识。为了探究不同电极过程的特性，往往需要得到宽频范围内的阻抗。在进行宽频阻抗估计时，低采样率无法捕捉短时间尺度的特性，而高采样率又会导致低频阻抗估计的数据饱和。针对此问题，多时间尺度的参数辨识方法是必须的(Dai et al. 2016，Weddle et al. 2018)。另外，估计宽频范围内的阻抗也需要谐波成分非常丰富的电压和电流工况数据。而且待估计的阻抗最高频率也对信号的最高采样速率有要求。这种高采样率受到了目前量产的BMS模拟前端的限制，而且在实车应用中也不得不考虑有限的数据传输带宽带来的影响。

4.2 测量阻抗测量是更为直接的阻抗获取方法。当电动汽车运行时，电池的工况和状态时刻在变，此时很难保证阻抗测量的线性、稳定性和因果性条件。文献中报道的阻抗测量多是在停车过程中完成。在此时，电池包内的温度分布不均、电池单体的均衡电流以及变换器的纹波等都是可控甚至可以忽略的。为了测量电池阻抗，一个具备激励发生、电压和电流信号测量、阻抗计算功能的系统是必须的。

(1)激励装置。电动汽车的动力电池组往往由很多串联连接的电池单体或模组组成，如图7。根据激励是加载到电池组还是单体电池两端，可分为集中式和分布式测量方案两种。集中式的方案可以对电池单体或模组同时激励，而分布式需要单独进行激励。两种方案都被较多地研究报道。前者多是集成于大功率的DC-DC变换器中，特别是充电机中。后者多是与主动均衡电路相结合，或者是类似恩智浦和松下提出的单芯片解决方案。相较而言，集中式方案能够提供更强的激励信号，对于大容量电池或模组更加适用。而分布式方案由于功率的限制，需要在信号检测精度方面具有更高的要求。

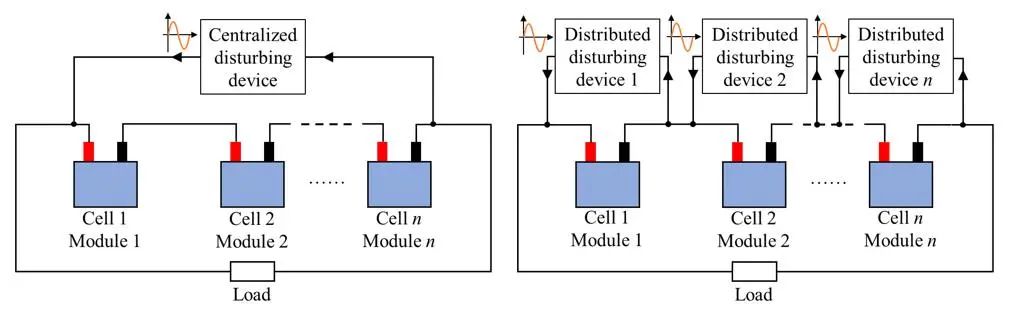
(a) (b)

图7 (a) 集中式和 (b) 分布式的电池阻抗测量方案

(2)激励信号。文献报道了很多可以用来进行阻抗测量的激励信号，包括单频率正弦、多频率合成正弦、方波、三角波、伪随机序列、阶跃信号等。这些信号被分成两种形式，一是包含单一频率的信号，这类激励信号可以容易保证测量过程中的信噪比，利于提升测量精度。但是由于各个频率依次叠加，对于宽频范围内阻抗的测量速度比较慢。这种激励形式适合实时性要求低且精度要求高的场合。在一些场合中，为了快速测量阻抗，包含丰富谐波成分的信号被用来作为激励。相比于单一频率信号，这类信号中的谐波成分幅值往往没有进行优化，会导致一些频率的谐波信噪比低，进而阻抗误差大。另外，过大的电流会导致电池的温度发生变化，直流电流的存在也会使得电池的SOC发生偏移。在选择激励信号时，应该注意不同幅值、直流电流和静置时间对阻抗的影响。

(3)电压和电流测量。通常为了保证线性和稳定性，阻抗是在小的扰动下测量。电池在激励电流作用下的响应电压在10mV左右。考虑三元电池本身的端电压在2.5-4.2V之间，直接在大电压偏置下检测微弱的响应电压对测量装置提出了非常高的精度要求。一般会采用去除直流分量的方法，并进一步放大交流响应电压来保证测量精度(Din et al. 2017，Dam 2016)。另外，为了准确的测量阻抗，按照香农采样定理，电压和电流的采样频率至少需要是被测阻抗最高频率的2倍。在实际的系统中，这个倍数会达到更高，为最高频率的5-10倍。这对模拟前端的采样速率提出了很高的要求。现有的电池管理芯片以监控电压为设计目的，目前仍无法满足此应用需求。而且在串联电池组中电池单体的电压和电流往往分别由电池组本地控制器和电池包中央控制器进行测量(图8)，不同控制器需要在测量前完成时钟同步，以确保不对计算的阻抗相位产生影响(Wei et al. 2018)。

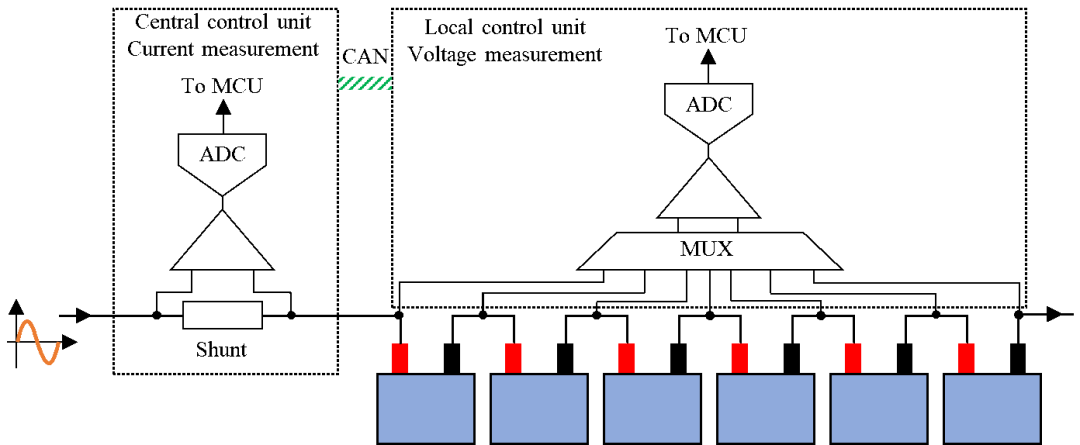
图8 串联电池组中的电压和电流测量方案

(4)阻抗计算方法。对于单一频率的正弦扰动，可以采用锁相放大器来提取电压和电流信号的幅值和相位来计算阻抗(Wei et al. 2018)，如图9。对于包含多频率的周期性谐波信号，可以采用傅里叶变换进行阻抗计算。而对于非周期的谐波信号，可以采用加窗傅里叶变换。由于加窗傅里叶变换的窗函数宽度固定，在进行多频率分析时难以实现窗口宽度与被分析信号频率的自适应。小波变换的方法也被应用于阻抗计算中。借助于小波变换强大的谐波提取能力，采用阶跃信号便可轻松实现宽频阻抗计算(Hoshi et al. 2016，Wang et al. 2019)，如图10。

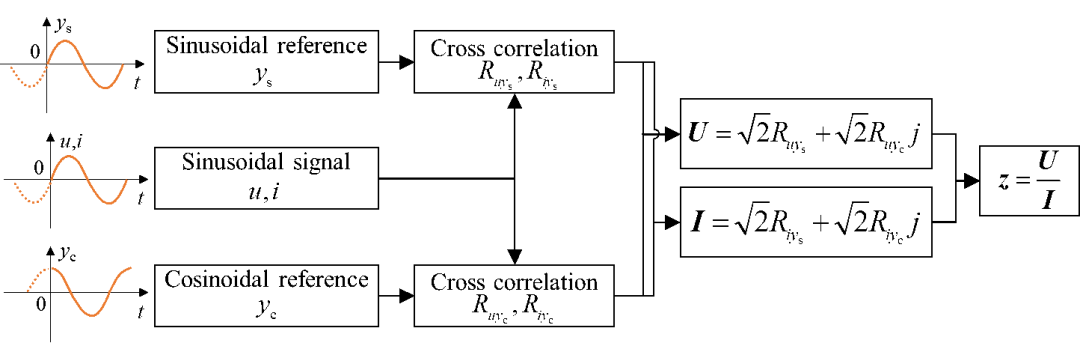
图9 基于互相关检测的阻抗计算方法

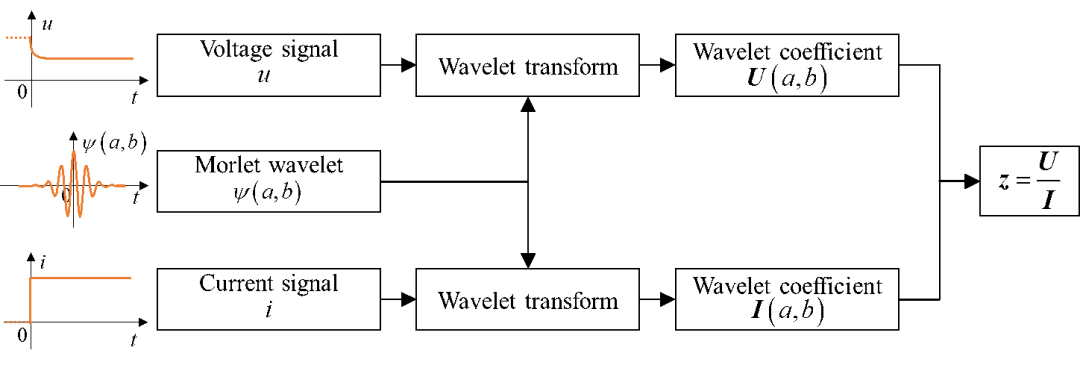
图10 基于小波变换的阻抗计算方法

(5)其它影响。阻抗的测量也不得不考虑其它一些影响因素。如图11，对于串联连接的电池单体或模组，他们的电压测量不可能像实验室进行EIS测量所采用的Kelvin接法的四线制一样，连接器与电池之间(B、C点)的接触阻抗上的分压将会被图中的1和2测量而无法与电池的端电压区分开来。当电池组出现连接故障时，接触阻抗会变化，使得测量得到的阻抗偏离真实阻抗。这个阻抗往往只对高频欧姆电阻产生影响。因此，一个简单的解决方法是直接将此接触阻抗作为电池的阻抗予以考虑。但是，在此方面的研究比较少。接触电阻如何对电池的阻抗应用产生影响需要进行深入研究。

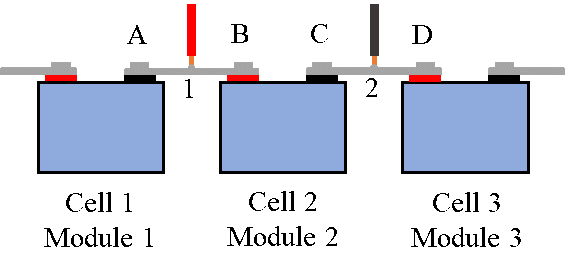
图11 串联电池单体或模组上的电压采样点

5 阻抗的应用

5.1 温度估计

温度对电池的性能影响很大。工作在不合适的温度下，电池将面临寿命、安全性的问题。因此对于BMS来说，实时监测电池温度对高效管理至关重要。采用传感器对温度测量是最直接的。这种方法多数只能实现极耳或表面的温度测量。但是，在高倍率充放电过程中，表面温度与电池内部温度差别很大。依赖表面温度监控仍然面临因内部温度过高导致的安全问题。因此，内部温度估计被广泛研究(Raijmakers et al. 2019)。基于阻抗进行温度估计是一条重要的技术路线(Beelen et al. 2020)。文献报道了利用四种利用阻抗进行温度估计的方法，即分别基于阻抗角、实部、虚部和与实轴相交处对应的穿越频率。已有的研究多数是在准稳态工况下获取阻抗来进行温度估计。但是，往往温度的变化在动态工况下是更加剧烈。动态工况对温度表征阻抗角的影响以及此方法在动态工况下的适用性仍缺乏足够的研究。

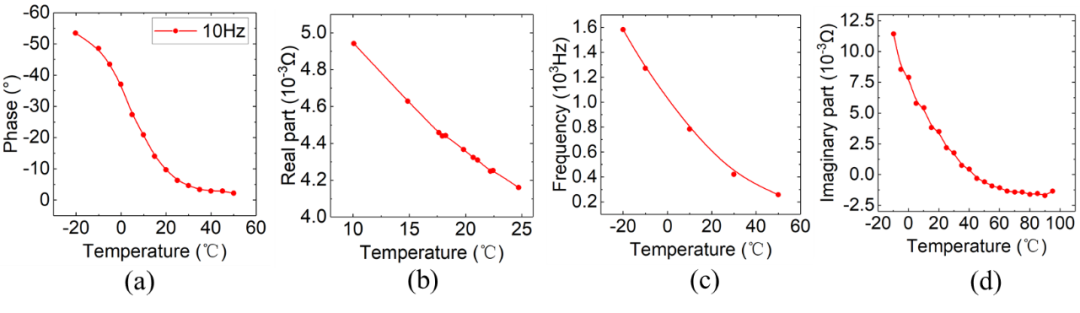
图 12 电池温度与(a) 10Hz阻抗角、(b) 10.3 kHz阻抗实部、(c) 阻抗谱在实轴上穿越频率和(d) 300 Hz阻抗虚部之间的关系

5.2 荷电状态估计

SOC的准确估计对防止电池过充和过放具有重要意义(Hannan et al. 2017)。对于基于模型的SOC估计方法，其估计精度往往受到模型精度和参数辨识算法的影响。特别地，对于例如磷酸铁锂电池，由于其具有非常平坦的SOC-OCV曲线，给基于模型的SOC估计带来了更大的挑战。阻抗作为一个与电池内部电极过充密切相关的量与SOC的关系也非常密切。很多基于阻抗的SOC估计方法被提出。文献报道了很多利用阻抗进行磷酸铁锂电池SOC估计的方法，显示该方法的有效性。但是，估计SOC而不打断电池的正常充放电过程很少在文献中报道。在此方面，仍有很多欠缺。

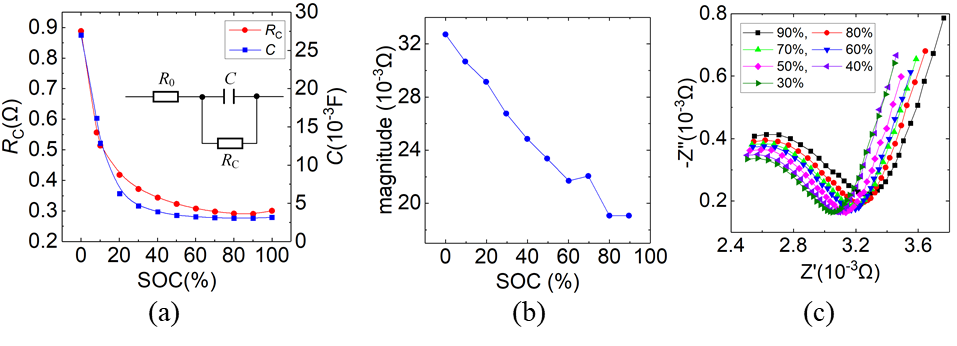
图13 SOC与(a) RC并联环节中的电阻、(b) 0.01Hz的阻抗模和 (c) 80 Hz - 0.1 Hz范围内阻抗谱

5.3 老化状态估计

电池老化状态估计对电池在线管理和退役残值评估都有重要意义(Xiong et al. 2018, Sarmah et al. 2019)。电池的老化是一个涉及很多过程的复杂现象。阻抗可以反映内部电极过程特性，采用阻抗进行SOH估计被大量报道。采用ECM分析不同老化阶段的电池EIS来进行SOH的估计是常用的技术路线。电池欧姆电阻、SEI电阻、传荷电阻等都可用来表征电池的老化状态。这些电阻从不同的维度描述了电池老化的过程。一些基于这些电阻的老化模式分析也被提出(Pastor-Fernández et al. 2017，Zhu et al. 2020)。对于实际的车载应用场景，电池的温度和SOC时刻变化，如何量化并排除这些因素对老化表征阻抗的影响仍然欠缺研究。

5.4 故障诊断

(1)过充和过放诊断。通过采用ECM对过放情况下的EIS进行拟合可以发现，欧姆电阻、传荷电阻、SEI电阻和Warburg电阻都发生了很大的变化(Liu et al. 2014)。进一步通过三电极实验发现，虽然负极对电池的阻抗贡献较小，但是在过放情况下对电池阻抗影响很大。文献也研究发现，在电池过充情况下，正极阻抗以及高频的负极阻抗都发生了明显变化(Liu et al. 2015，Love et al. 2012)。

(2)析锂诊断。在大倍率充电或者低温充电时容易诱发析锂，是导致电池安全性和寿命变差的重要原因。实现对析锂的在线检测具有重要意义。研究发现，在大倍率充电结束后电池阻抗的变小与析锂有关(Schindler et al. 2016)。且充电过程中的3s直流电阻随SOC变化的趋势的改变也与析锂相关(Koleti et al. 2020)。

(3)内短路诊断。内短路是造成电池热失控的重要原因之一。Kong等人采用电池外部并联电阻来模拟电池内短路的漏电流，并分析了不同漏电流下电池不同频率阻抗的变化(Kong et al. 2020)。发现漏电流越大，电池低频扩散段的阻抗会向实轴弯曲且影响越明显，为内短路的诊断提供了思路。

【结论】

通过对阻抗建模、获取和应用方面的进展回顾，可以看到阻抗在电池管理研究中被频繁报道且有宽阔的应用前景，但是仍然有很多的工程和科学问题需要解决，具体如下：

(1)电化学阻抗模型复杂且参数多，等效电路模型更适于面向控制的应用。但是等效电路模型形式千变万化，需要合理选择具有明确物理意义和精度的阻抗模型并提出面向控制的参数辨识方法以实现所获取的阻抗的解析。

(2)电池阻抗可以通过估计和测量两种途径获取，前者受到模型精度、工况的谐波丰度以及多时间尺度辨识方面的挑战。后者是更加直接、有效的方法，但是仍需要攻克高精度、高速度的模拟前端以及低成本、高兼容性系统实现等方面技术难题。

(3)电池阻抗对电池状态和故障非常敏感，也使得阻抗具有宽阔的应用场景，目前已经开展了大量研究。但是仍需要进一步揭示并去除状态估计或故障诊断中其它因素对特征阻抗的影响以提升对车载复杂工况的适用性。

对上述问题的解决，将扩展阻抗的应用场景，使之从实验室走向车载，对发展更加智能的BMS具有重要意义.

审核编辑：汤梓红