基于开关平均化模型的PFC电路仿真

摘要：采用开关器件的平均化模型，根据实际电路工作原理，建立适用于PSPICE软件的PFC电

路仿真模型。采用此模型进行仿真、具有速度快、实现简单且与实际电路结合密切的特点。

模型的准确性由所建模型与实际电路模型仿真结果的比较得到证实。

关键词：PFC仿真平均化

1引言

　　在电力电子系统的研究中，仿真研究由于其高效、高精度及高的经济性与可靠性，而得到大量应用。近二十年来，仿真已逐渐成为电力电子CAD的有力工具。当前，PFC电路是电力电子研究领域的一个热点，对于PFC电路本身来说，具有非线性和时变的特性。电路的仿真研究，对于电路分析和参数优化选择具有重要意义，极大地方便了电路设计。但由于PFC电路工作频率较高，若采用PSPICE软件进行瞬态仿真，电路开关周期限制了仿真步长的取值。同时，由于PFC电路控制采用双环结构，电路结构复杂。这样，就占用了大量的机时。使仿真的高效性大打折扣。鉴于此，文献[1]提出了基于系统建模法的PFC电路模型仿真。该模型用受控源实现了电路的数学模型描述式，模型与实际电路无密切联系。且模型假设电路功率因数为1，从而使电流控制环特性无法在模型中得到反映。本文利用开关的平均化模型代替开关模型，并利用PSPICE软件丰富的受控源器件建立了PFC电路的双闭环仿真模型。该模型与实际电路结构密切结合，且大幅度减少了仿真占用机时，提高了仿真效率。在本文中，将采用开关器件物理模型的PFC电路仿真模型简称为开关模型，将采用开关器件平均化模型的PFC电路仿真模型简称为平均化模型。

2开关的平均化模型

　　利用PSPICE软件对电路开关模型进行瞬态分析时，在每一个开关时刻都要进行一次电路状态方程的求解。由于PFC电路工作频率较高，所以，电路的仿真要占用大量机时。而通过建立开关平均化模型，在电路开关周期小于电路时间常数的条件下，利用低频，平均化等效电路（如受控源）代替变换器中的开关器件，使仿真过程避免了在每一个开关时刻求解电路状态方程，从而提高了仿真速度。

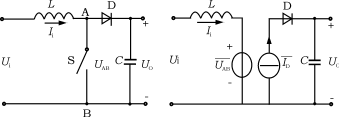
（a）开关物理模型（b）开关平均化模型

图1电路仿真模型

　　对于图1(a)所示的电路结构，当电感电流连续时（CICM），在一个开关周期内，设开关的占空比为D，开关S两端电压平均值为：

UAB=(1－D)Uo(1)

流过二极管的电流平均值为：

ID=(1－D)IL(2)

基于式（1）（2），我们可分别用受控电压源代替主开关，用受控电流源代替续流二极管，得到原电路在一个开关周期内的平均化模型。与原电路相比，输入电感两端平均电压与经续流二极管流入电路末端的平均电流保持不变。

　

3PFC电路仿真模型的建立

3.1主电路模型

　　我们采用开关平均化模型代替PFC电路主开关和续流二极管，其余电路元器件仍采用实际电路模型。这样的好处在于使仿真电路最大限度地与实际电路保持一致。

3.2控制电路模型

　　对于采用平均电流控制的PFC电路来说，其控制器为双环结构。其中由电压外环决定电流内环参考信号，使电路输入输出功率保持平衡。通过电流内环控制开关通断，使输入电感电流实现对电流参考信号的精确跟踪。在实际电路中，电流内环参考信号是由电流与电压同步的信号KUIN、电压外环调节器输出AV.out、和输入电压有效值URMS三路信号按式（3）综合后得到的[2]：

IREF=KUINAVOUT/U2RMS(3)

在电路模型中，我们利用乘法器实现了上式。对于1/U2RMS项，电路须做一次平方和一次除法运算，这将使仿真模型的复杂性和仿真占用时间增加。为此，在建模中采用离线计算，然后将其作为式（3）的相乘因子。对于电流调节器，模型与实际电路一致。在实际电路工作时，由电流调节器的输出与稳定的锯齿波进行比较来控制开关通断。在受控源模型中，由于电流调节器输出不含开关频率脉动，假设稳定的锯齿波幅值为5V，代替主开关和续流二极管的两个受控源控制式中均含有的因子（1－D）可表示为，

　　（1－D）=1－Ai.out/5(4)

在PSPICE元件库中，表格式电压受控源可以按照数学表达式对控制信号进行运算。在此，我们用一个表格式电压源实现式（4）。最后，加上电压调节器就完成了整个系统模型的建立。完整的模型如图2所示：乘法器电压源E1代替了主开关，乘法器电流源G1代替了续流二级管。式（3）由乘法器电压源E2和乘法器电流源G2实现，式（4）由表格式电压源E14实现。在模型中用到了电流控制电压源H1，主要是用来把电流信号转换为适合受控源输入信号要求的电压信号。

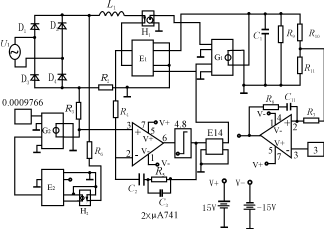
图2PFC电路平均化仿真模型

4仿真结果分析

　　为了验证平均化模型的准确性，将电路开关模型与平均化模型仿真结果进行了对比。仿真是利用PSPICE软件进行150ms的瞬态分析，开关频率为100kHz。从仿真结果看，对于开关模型的动态过程中，电压峰值为81.4V，稳态时，电压脉动为8.4V，输出电压平均值为73.6V，输入电感电流峰值为4.8A。对于平均化模型的动态过程中，电压峰值为80.8V，稳态时，电压脉动为8.3V，输出电压平均值为73.4V，输入电感电流峰值为4.76A。由于仿真结果的差别非常小，所以我们有理由认为，平均化模型有很高的可信度。

（a）开关模型结果    （b）受控源模型结果

图3PFC电路输入电流波形频谱分析

　　前已叙及，平均化模型是开关电路的低频等效模型。所以，对于低频信号或信号中的低频成分，两种模型应当等效，为此，我们对PFC电路仿真结果中的网侧输入电流波形进行了傅立叶分析，由于信号所含的频率在1kHz到开关频率之间的成分近似为零，所以，我们截取1kHz以下的频谱进行对照。结果见图3，其中（a）图为电路实际模型输入电流频谱，（b）图为平均化模型输入电流频谱。两图对照几乎重合。以50Hz为中心频率进行分析，结果表明，（a）图中心频率傅立叶系数为4.57A，谐波含量为6.2％，（b）图中心频率傅立叶系数为4.46A，谐波含量为5.9％。可以证明两个模型的低频等效性。

　　然而，最令人振奋的是两种模型仿真占用机时的比较。在奔腾300微机上做150ms瞬态分析，采用开关模型共花费2小时13分，而采用平均化模型只用了25秒。后者速度为前者的数百倍。这对于电路参数（如调节器）的仿真优化尤为可贵。但由于电路开关过程的平均化，一些瞬态参数如电感电流脉动，开关器件承受的瞬态电压（流）等不能在仿真结果中表现出来，这可以从原始模型仿真结果中得到。此外，从仿真

　

波形上看，受控源模型仿真曲线不光滑，可能是由于两种模型高频特性的差异造成的。

5结论

　　本文利用开关器件受控源模型代替开关器件模型，并结合电路实际工作原理建立了工作于电感电流连续模式（CICM）的PFC电路平均化仿真模型。该模型与开关模型相比，有以下特点：

（1）在保证仿真准确度的前提下，提高速度数百倍。

（2）与实际电路结合密切，减小了由于模型引起的仿真与实验结果差异，提高了仿真的可信度，也便于利用仿真实现电路参数优化。

参考文献

1王燕等，基于系统建模法的PFC电路仿真，电力电子技术,1999年第1期。

2PhlipsTUC3854ControlledPowerFactorCorrecTIonCircuitDesign,UnitrodApplicaTIonNote,1994.pp303－322.