ML4835复合PFC/CFL小型荧光灯基于Matlab的电力电子电路仿真方法
摘要:介绍了一种使用Matlab仿真电力电子电路的一般性方法。该方法可以得出电力电子电路的大信号非线性仿真模型,为电力电子电路的仿真研究提供了一种方便、快捷的手段。
关键词:仿真非线性模型Matlab
1前言
Matlab软件应用广泛,特别是它的可开发的Simulink工具箱给各行业的工程技术人员提供了便捷的实验手段。对于电力电子拓扑,由于它的非线性可以使用Simulink中的开关模拟,因此通过分段分析电路拓扑,然后使用开关来切换各段电路就可以得出一个完整的电路的仿真模型。本文以Sheppard?Taylor拓扑[1]为例叙述其实现方法及应注意的问题,最后给出结论。
2建立非线性仿真模型的一般性规则
在电力电子电路中通常含有高频开关(如MOSFET等),给电路引入了非线性。对此类非线性,在分析电路时比较常用的方法是状态空间平均法[2],即首先对电路的一个开关周期进行分段,如果电路中的电感电流工作在连续模式下,则分成Ton和Toff两段;否则分成Ton、Toff1和Toff2三段。然后分段对电路中的储能元件(如L、C)列写状态方程式。当电感电流连续时有两组状态方程,电感电流断续时有三组状态方程。最后对所列状态方程组按开关动作占空比和电流断续时间比(电流断续时)做加权平均,形成一个新的状态方程组,并基于此对电路进行分析。由于它抓住了高频开关动作对低频元件的加权平均等效性,可以较好地描述电路特性。状态空间平均法的优点是:可以得到代数描述,便于系统分析和综合。不足之处在于它的出发点是线性展开,因而得到的是小信号模型,且过程较繁。本文针对它的不足,利用Matlab求解非线性方程的能力,根据非线性方程组直接构造大信号仿真模型,并基于此对电路进行分析。
2?1建立非线性方程组
此过程采用基本的电路方法,毋庸赘述,下面以例示之。对于图1所示Sheppard?Taylor电路(两开关同时动作)按电感L1电流断续而电感L2电流连续分别可得状态方程组: =Aix+Biu(i=1,2,3)(1)
=Aix+Biu(i=1,2,3)(1)
式中: x=[iL1,uC1,iL2,uO}T u=US A1=
A1=

图1Sheppard?Taylor拓扑

图2关联矩阵关系的实现

图3Sheppard?Taylor拓扑非线性仿真模型的Matlab实现
 A2=
A2= A3=
A3=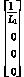
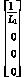
 B1=B2=B3=
B1=B2=B3=
2?2建立非线性关联矩阵E,F
E=[mI?pI?qI][A1?A2?A3]T
=mA1+pA2+qA3(2)
F=[mI?pI?qI][B1?B2?B3]T
=mB1+pB2+qB3(3)
式中:[mI?pI?qI]为n×3n矩阵
[A1?A2?A3]T为3n×n矩阵
[B1?B2?B3]T为3n×n矩阵
n为Ai的阶数。
2?3构造仿真模型
由于电路工作时是在状态方程组中分时切换,因此可以通过式(1)、(2)、(3)得到非线性仿真模型: =Ex+Fu(4)
=Ex+Fu(4)
式中E,F如公式(2)、(3)。
仿真模型(4)在形式上与状态空间平均法虽有相似之处,但存在本质的差异。本方法在构造出模型(4)时没作任何忽略和线性近似(状态空间平均法是基于小纹波近似),因此是非线性大信号模型。
3关联矩阵的实现
上述仿真模型可以使用Matlab的Simulink工具箱方便实现。值得指出的是切换阵[mI?pI?qI]的实现。在本质上m,p,q是切换时间,其中m取决于开关占空比D,而p,q的总和为开关的占空比D′(D′=1-D)。但p,q的切换时刻与状态和电路参数有关。使用switch开关描述的关联矩阵的实现方法如下:
开关切换如图2所示。使用一个脉冲发生器来模拟开关占空比D。switch2当5路信号为高时选通1路,否则选通4路。因此对于m,p之间的切换发生在脉冲发生器的高低电平变换时。而对于2路和3路的切换,根据电路电感中电流的断续点进行,switch1当工作在断续状态的电感中有电流时选通2路,否则选通3路。其中开关switch1和switch2的阈值分别设为0和1即可。
4基于Matlab仿真实现和结果
以图1拓扑为例,当其工作在DCM?CCM方式时,电感L1工作在断续模式,而电感L2工作在连续模式,两MOSFET管工作在同步状态(即同时开通、同时关断)。当MOSFETS开通时,电源给电感L1储能,电容C1给负载提供能量;当MOSFETS关断时,电感L1的能量经D1,D2流入电容C1给其充电。在其中某一时刻电感L1的电流下降为零,而电感L2一直工作在连续方式。仿真模型具体的Simulink实现如图3所示。
用图3进行仿真可以直观地得出电感L1、L2的电流波形和电容C1、C2上的电压波形,且电容C2的
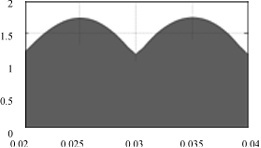

图4仿真结果
(a)电感电流iL1的周期波形(b)电感电流iL1的局部放大波形
电压即是输出电压。从图4(a)、图4(b)电感L1的电流可以看出电感L1是工作在断续状态且实现了PFC。图4(a)中在nπ(n=1,2,3...)时刻电流未到零主要是其工作在断续开环的缘故。
电路参数如下:L1=300μH,L2=735μH,C1=270μF,C2=1000μF。输入US=110|sin(100π)|,工作频率是fs=100kHz,D=0.169。
从图4(c)、图4(d)可以看出非线性模型的结果与平均模型的稳态结果(图略)吻合的很好。
5结语
使用状态空间平均法可以获得非线性开关系统的小信号线性化模型,但是推导较复杂。本文通过建立电路的状态方程组,获得非线性仿真模型,然后使用Matlab进行分析。此方法具有以下的一些优点:该模型是基于电路的原始非线性方程,是一个完全的非线性系统,具有大信号模型的特点。使用该方法的另一个显著的优点是构造简捷。只需要通过对电路列出两组(电流断续三组)方程,然后使用Simulink中的switch开关就可以方便地构造出来,并可以很直观地获得电路的仿真结果,对电路的CAD具有一定指导意义。不足之处是本方法属于结构性描述而非代数描述,不适于系统综合。
200多个MATLAB经典教程和MATLAB论文请查看:matlab教程