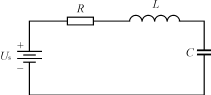
|
谐振技术及其应用 摘要：首先介绍了硬开关电路的缺陷，引出谐振技术，然后详细分析了基本电路在不同的初始条件下的工作情况，接着分析了谐振参数间的关系及其会带来的问题。最后，介绍了该技术的应用，同时分析该技术在变换器中存在的问题。 关键词：硬开关；软开关；谐振技术 Resonant Technique and Its ApplicaTIon SUN Ze, WANG Gang Abstract:The faults of hard switching circuit are first analyzed, then the resonant technique by using a basic circuit is introduced and the relaTIon between the resonant parameters and quesTIons produced possibly are analyzed. At last, its applicaTIon and existing questions in converter are presented. Keywords:Hard switching; Soft switching; Resonant technique 中图分类号：TN86文献标识码：B文章编号：0219－2713(2002)3－0093－04 1 引言 在开关电源中，通常采用磁性元件（如铁心电感、变压器等）实现交流/直流侧的滤波，能量存储和传输。这些磁性元件在电源装置的体积、重量、成本中占有很大比重。开关器件的工作频率越高，磁性元件的尺寸就可以越小，电源装置的小型化、轻量化、低成本化就越容易实现。但是，传统的PWM变换器中的开关器件工作在硬开关状态，存在很多缺陷： 1）开通和关断损耗大； 2）感性关断问题； 3）容性开通问题； 4）二极管反向恢复问题。 由于硬开关工作时存在上述四大缺陷，所以使开关器件工作频率的提高受到限制，从而电源装置的小型化、轻量化、低成本化也就不易实现。克服以上缺陷的有效办法就是应用软开关（SoftSwitching，简称SS）技术。最理想的软开通过程是：电压先下降到零后，电流再缓慢上升到通态值，所以导通损耗近似为零。另外，因器件导通前电压已下降到零，器件结电容上的电压亦为零，因而解决了容性开通问题，这意味着二极管已经截止，其反向恢复过程结束，因此二极管反向恢复问题亦不复存在。最理想的软关断过程是：电流先下降到零，电压再缓慢上升到断态值，所以关断损耗近似为零。由于器件关断前电流已下降到零，即线路电感中电流亦为零，所以感性关断问题得以解决。事实上，这两个过程要么存在感性关断问题，要么存在容性开通问题。也就是说，仅仅利用一个电感或电容是不能根本解决问题的，所以最好的情况应当是使开关在电压和电流同时为零时关断和开通，损耗才会真正为零。而要实现这个目标，就要用到谐振技术。 2 谐振技术 2.1 谐振过程 根据电路原理，电感电容串联或并联可构成谐振电路，使得在电源为直流电源时，电路中的电流按正弦规律变化。由于电流或电压按正弦规律变化，存在过零点，如果我们能够在这一时刻开通或关断，产生的损耗就为零。下面就分析电源里用得最多的二次串联谐振电路，对其在初始情况不同时的工作情况进行讨论。基本电路如图1所示。
假定电容C上的电压为uC，电感L中的电流为iL，电源电压为Us。于是，该电路的微分方程为： L(di/dt)＋Ri＋uc=Us （1） i=C(duc/dt) （2） 将式（2）代入式（1），得 LC(d2uc2/dt2)＋RC(duc/dt)＋uc=Us （3） 式（3）对应的齐次方程为： LC(d2uc2/dt2)＋RC(duc/dt)＋uc=0 （4） 该齐次方程对应的特征方程为： LCs2＋RCs＋1=0 （5） 在R< s1=－β＋jω′ s2=－β－jω′ （6） 式中：β=R/2L； ω′= ω0= 于是，式（4）的解为： 很显然，uc=Us是方程的一个特解，即 可得，式（3）的通解为： uc=y= =e－βt(A1cosω't＋A2sinω't)＋Us （9） 下面分别讨论该电路在不同初始条件下的解以及相应的电压电流波形： 1）第一种情况 初始条件为：iL=0，uc=0。方程的解为： uc=－ iL=e－ βtsin(ω't) （11） 波形如图2所示。
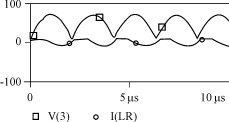
2）第二种情况 初始条件为：iL=0，uc=U0。方程的解为： uc= iL=－e－βtsin(ω't) （13） 波形如图3所示。
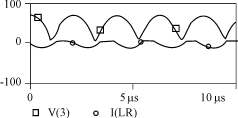
3）第三种情况 初始条件为：iL=I0，uc=U0。方程的解为： uc= iL=－ 波形如图4所示。
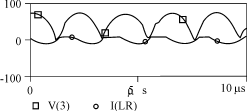
4）第四种情况 初始条件为：iL=I0，uc=0。方程的解为： uc=－ iL= 波形如图5所示。
2.2 公式分析 上述公式中，β为衰减常数，e－ βt即为衰减项，ω'为固有周期。如果β越大，e－ βt衰减就越快。一般来说，这是我们所不希望的；如果要使衰减变慢，那么就要减少β，即减少R/2L。其实，对高频开关来说，在几个μs甚至更少时间里，其衰减是非常微小的，可不予考虑。至于固有周期可根据需要，调整L和C的大小，使得ω'满足要求，即在要求的时间里给电容充电到某一值或使电流过零点。另外，从ω0= 3 实际应用 谐振技术应用到开关电源中时，可根据各电源的拓扑结构的特点，再结合设计者的要求（是否要让电感中的电流经过一定时间后为零，再关断器件），采用上面四种情况中一种或几种构造出相应的电路，得到相应的谐振变换器。下面举例分析其应用： 1）用第三种情况实现Buck电路开关的零电流关断。电路拓扑如图6所示。
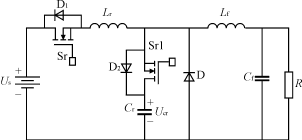
相关工作情况分析：开关Sr断开时，二极管D续流。当开关Sr闭合后，iLr线性上升，续流二极管D中的电流则线性下降。当iLr=Io时，二极管D截止。Cr开始通过Lr和D2充电。此时，Cr和Lr串联谐振。在iLr上升到最大值后再下降到I0后，D2截止（受反压）。经过一个恒定阶段后，开关Sr1导通，Cr开始放电，iLr逐渐减小至零并变负。如果在过零点关断开关Sr，损耗将为零。这就是我们要得到的零电流关断电源。 2）用第三和第四种情况在降压软开关——PWM变换器中的应用。其电路拓扑如图7所示。
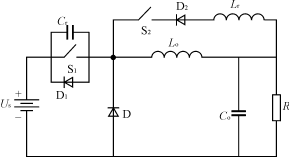
其工作情况为：在S1和S2均关断时，续流二极管D导通。开通S2，于是Lr中的电流线性增加经过一段时间达到Io。此时，续流二极管D截止，Lr和Cr开始谐振，Cr两端的电压逐渐下降，经过一段时间降为零，在此时D1导通，谐振电流线性下降。如果在这个期间开通S1，实现的是零电压开通。接着，谐振电流继续下降，当下降到Io时D1截止。由于S1已经开通，ir仍将继续下降直至零。关断S2，即以零电流关断，损耗为零。 4 问题分析 谐振变换器是最适应高频化的电路，但是在使用谐振变换器时，必须解决以下几个问题：其一，频率固定情况下，电压难以调整；其二，开关器件的应力问题；其三，L和C的发热问题。其中，电压调整的问题最难解决。通过开关的电流宽度ton（对于电流谐振方式），以及加在开关上的电压宽度toff（对于电压谐振方式），都分别由谐振电路确定。因此，要控制占空比D，就必须改变周期T，即开关频率f。然而，改变开关频率也将伴随着开关通断产生的噪声谱的改变，这就不利于噪声的抑制。另外，决定变换器体积的磁性元件和电容器要按最低频率设计，这样就未必能小型化。电流谐振时，正弦波的输出电流峰值随负载成比例增大。因此，开关器件的耗散功率与驱动功率随之增大。电压谐振时，截止状态加在开关上的电压波形的峰值也随负载增大，因此，需要选用高耐压的开关器件。为此，可采用辅助开关对电流或电压进行箝位，以减轻开关器件上的应力。对于谐振变换器，除了加在开关器件上的应力以外，还有构成谐振电路的L和C的负担问题。特别是重负载，L与C上加上过高电压，使电流的振幅增大，从而高频损耗增加。所以，为控制L的发热和实现小型化，要开发高频特性好、热阻抗低，而且能确保一定导磁率和矫顽力的磁性材料。另外，要开发对高频有足够的电流容量、等效串联电阻足够小的电容。 5 结论 只要认真研究开关电路的特点，结合电容、电感串并联在不同初始条件下工作的特点，构造出相应的电路，应用到变换器中，以实现不同的技术要求。此外，还应当注意克服谐振带来的负面影响，如元器件的电压应力变大，可应用箝位技术加以限制。 参考文献 [1] 杨德刚,赵良炳.软开关技术回顾与展望[J].电力电子技术,1998. [2] 周仕祥,黄是鹏.改进的降压型软开关PWM变换器.电工技术学报[J]，1997. [3] 张占松,蔡宣三.开关电源的原理与设计[M].北京：电子工业出版社.1999. [4] 王英剑,常敏慧,何希才.新型开关电源使用技术[M].北京：电子工业出版社.1999. |
条件下，求得方程的解为：
；
。
=e－βt(A1cosω′t＋A2sinω′t) （7）
＋
e－βtsin(ω't＋ arctan
)＋Us (10)
e－βtsin(ω't＋ arctan
)＋Us (12)
e－βtsin(ω't＋arctan
)＋
e－βtsin(ω't)＋Us (14)
e－βtsin(ω't)－
e－βtsin(ω't－ arctan
) （15）
)＋
e－βtsin(ω't)＋Us (16)
e－βtsin(ω't)－
e－βtsin(ω't－ arctan
) （17）
可知：电感和电容的值越小，谐振频率越高；从ω0/ω'=
=
可知：在电阻R一定的情况之下，电容与电感的比值越小，1－R2C/4L就越大，ω0/ω'值就越小。反之，电容与电感的比值越大，1－R2C/4L就越小，甚至趋近于零，ω0/ω'就会变得非常大。因此，在谐振频率一定的情况下，电容和电感的值一定要合适，尽量使ω0/ω'小。当谐振技术应用到开关电源中，在初始条件不为零时的解，可能会再叠加一个大于某值〔该值同初值相等或相当，如Us，U0－Us，见式（12）～（17）〕的值，使开关的应力增加，同时使开关的损耗也加大。
