摘要：在机器人手眼系统位置控制中，用CMAC神经网络建立了机器人非线性视觉映射关系模型，实现了图像坐标到机器人坐标的变换。该模型采用了一种新的多维CMAC网络的处理方法——叠加处理法。实验，与BP网络相比，CMAC网络能以罗高的精度和较快的速度完成手眼系统的坐标变换。

近年来，在智能机器人领域，关于机器人手眼系统位置控制问题的研究受到越来越多的关注。在研究中发现存在这样一个问题，即如何以较高的精度和较快的速度实现机器人手眼系统位置控制，以使机器人能快速实现对目标物体的准确定位和自动抓取。这个问题也就是机器人手眼系统中非线性视觉映射关系模型的建模问题。采用精确的数学模型是机器人视觉系统传统的建模方法。但由于这类问题是高度的非线性问题，参数多且其间的相关性强，故这种方法理论上虽然精确，但是建模困难、计算量大，实时性差且没有容错能力和自学习能力，而神经网络作为一种智能信息处理的新技术，具有极强的非线性映射能力。因此采用神经网络的建模方法与传统的方法相比具有极大的优越性。

作者已经采用BP网络建立了机器人视觉系统的映射模型，并作了初步的研究和实验。结果发现，采用神经网络建立机器人视觉映射模型是一种有效的建模方法。但采用BP网络建立模型存在网络规模大、训练时间长、容易陷入局部最小解、定位精度较低等缺点。本文采用CMAC神经网络建立了机器人视觉系统的映射模型，取得了十分令人满意的效果。

1 CMAC神经网络简介

小脑模型关节控制器神经网络(Cerebellar Model ArticulaTIon Controller Neural Network，即CMAC神经网络)是Albus根据小脑的生物模型提出的一种人工神经网络。它学习速度快，具有局域泛化能力，能够克服BP网络容易陷入局部最小点的问题，且硬件易于实现。目前，CMAC神经网络被广泛应用于机器人控制、非线性函数映射、模式识别以及自适应控制等领域。

1.1 CMAC的基本结构和原理

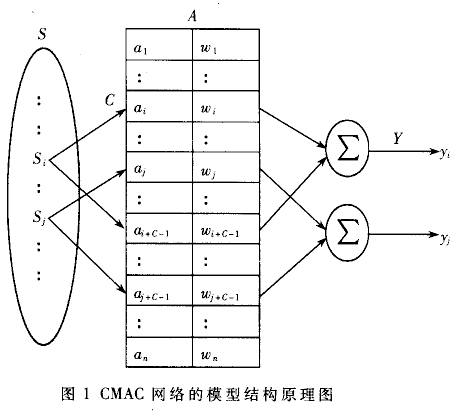
CMAC神经网络的模型结构原理图如图1所示。它本质上可看作是一种用于表示复杂非线性函数的查表结构。

图1中，S为n维输入矢量空间；A为联想记忆空间；Y是输出响应矢量。输入空间S中的每一矢量S(…，Si，…，Sj，…)被量化后送人存锗区A，每个输入变量Si激活存储区A中C个连续存储单元。网络输出yi为这C个对应单元中值(即权wi)的累加结果，对某一输入样本，总可通过调整权值达到期望输出值。由图1可以看出，每一输入样本对应于存储区A中的C个单元，当各样本分散存储在A中时，在S中比较靠近的那些样本就会在A中出现交叠现象，其输出值也比较相近，即这C个单元遵循"输入相邻，输出相近"的原则，这种现象被称为CMAC神经网络的局部泛化特性，C为泛化参数：C越大，对样本的映射关系影响越大，泛化能力越好。

CMAC网络的学习采用误差纠正算法，计算量少敛速度快。其权值修正公式及输出可表示如下：

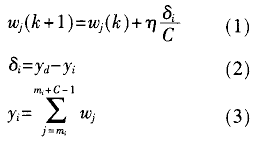
式中，η为学习步长，yd为期望输出，mi为输入变量S激活存储单元的首地址。修正方法可以采用每个样本修正一次的增量学习方法，也可以采用所有样本都输入一轮后再修正的批量学习方法。

1.2 多维CMAC网络的计算方法

由上述CMAC模型的算法可知，应用传统的多维CMAC概念映射算法会因输入维数的增大而使存储空间剧烈增大，从而使网络计算量增大，收敛速度变慢。这里采用一种新的多维CMAC网络的处理方法--叠加处理法。即把输入空间为n维的多维CMAC网络看作是由n个一维CMAC网络叠加而成，其输出为n个一维子网络的输出的叠加。\par

当输入空间的维数n=1时，对于每一个输入变量，都激活C个连续存储单元，即有C个对应单元的权值输出非零。它的激励情况如表l所示。

表1 激活单元地址分布

si	a1	a2	a3	a4	a5	a6	a7	a8	a9	a10
0	1	1	1	1	0	0	0	0	0	0
1	0	1	1	1	1	0	0	0	0	0
2	0	0	1	1	1	1	0	0	0	0
3	0	0	0	1	1	1	1	0	0	0
4	0	0	0	0	1	1	1	1	0	0
5	0	0	0	0	0	1	1	1	1	0
6	0	0	0	0	0	0	1	1	1	1

?

经归纳，输入变量Si激活存储单元的首地址mi的计算方法如下：

mi=Si(C-Δ)+1??? (4)

其中，Si为输入量的量化值；C为泛化参数；△为相邻输入激活存储单元的重叠单元数大小。若输入矢量有q个量化级，则存储区A需要q(C-△)+C个存储单元。．

当输入空间的维数n>1时；设输入空间为n维矢量Si=(Si1，Si2，…，Sin)，对于每个分量Sij，都可以看作图1所示结构模型的一维输入量。由式(3)可得其对应的输出为：

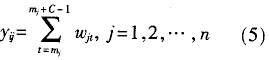
其中，mj为Sij所激活存储单元的首地址。整个CMAC网络可看作由n个如图1所示的子网络组成，S对应的输出yi可看作n个子网络输出yij（j=1，2，…，n）的叠加。

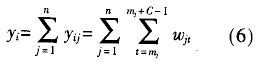
若每个输入分量有q个量化级，每个子网络中两相邻样本有△个单元重叠，采用上述叠加方法共需存储单元n×[q(C－△)+C]。而对于传统的多维概念映射算法来说，n维输入空间中可能的输入状态为qn个。对于一些实际系统，qn往往远远大于n×[q（C－△）+C]。例如8维输入，量化级为200个等级，泛化参数C取为40，相邻输入激活存储单元的重叠单元数大小△为35，则用叠加处理法需要11200个存储单元，而用传统的概念映射算法需要2008个存储单元。对于传统的概念映射算法所带来的要求存储空间过大的问题，最常用的方法是把A当作一个虚拟存储区，通过散射编码映射到一个小得多的物理空间单元Ap中，从而减少存储空间。但是这种地址压缩技术随机性很强，会带来冲撞问题且不可避免。然而，对多维CMAC网络采用叠加处理法，不但可以大大减少占用的存储单元数，而且还可以避免地址压缩带来的冲撞现象，大大提高网络的映射精度和学习速度。

图2

2 实验及仿真结果

实验是在山东大学现代物流实验中心进行的。该机器人手眼系统由用于抓取物体的SK6机械手和用于视觉定位的Panasonic WV-CP410／G彩色摄像头组成。摄像头采集的图像是二维的，而机械手运动到某一位置需要六自由度坐标。因此必须把二维图像坐标转换成机器人运动空间的六维坐标，才能控制机器人运动到指定的空间位置，这就是机器人手眼系统位置控制问题。本文采用CMAC神经网络实现了这一坐标变换，并对其结果与BP网络进行了比较。

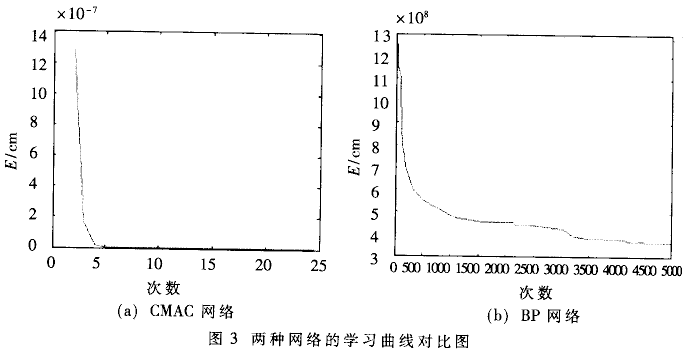
??? 本实验共采集到793个输入样本，选取CMAC网络的量化精度Q为1000，泛化参数C为80，学习步长η为0．30。图2(a)和(b)分别为对CMAC网络训练25次和对BP网络训练5000次的误差平方和曲面图。可以看出，CMAC网络在训练次数少于BP网络的情况下，其误差平方和远远小于BP网络，且误差分布比较均匀。图3(a)和(b)分别为CMAC网络和BP网络的误差平方和随学习次数的增加而变化的曲线图。由图可知CMAC网络的学习速度较BP网络有较大提高。