CAN总线技术在CFA6470型混合动力汽车中的应用

提出了一种第二代小波变换与SPIHT算法相结合在图像无损压缩中的编／解码方案，给出了本方案的实验结果及与其他方法的压缩性能比较，研究表明这一方法对于医学图像具有较高的无损压缩率。
    关键词：第二代小波变换，无损压缩，SPIHT，医学图像
1　引　言
　　随着社会的发展和医疗技术的进步，人们对身体健康的关心程度越来越高。医学影像已经不再是仅供医生参考的信息而成为诊断疾病的重要依据。在网络传输条件下的图像压缩编码成为建立数字化医院的关键技术。目前，二维图像的压缩标准有JPEG、GIF及采用了小波变换的JPEG2000等。医学图像具有特殊性，它一般不允许丢失有用的细节信息。传统的DCT（Discrete Cosine Transform，离散余弦变换）和第一代小波在图像变换后会产生浮点数，因而必须对变换后的数据进行量化处理，这样就会产生不同程度的失真。可见，量化器的设计是决定图像保真度的关键环节。由于第二代小波采用提升方法能够实现整数变换，因而能够实现图像的无损压缩，显然，它是一种很适于医学图像的压缩方法。
2　SPIHT算法
　　基于分层树的集合划分算法（Set ParTITIoning inHierarchical Trees，SPIHT）改进了内嵌零树编码算法（EZW）。在对图像进行小波变换后，它更有效地利用了不同尺度子带重要系数间的相似性。它呈现出良好的特性：不依赖傅立叶变换而在空间域中构造小波；较高的PSNR（Peak Signal Noise RaTIo，峰值信噪比）保证了良好的重现图像质量；整数运算利于实现实时快速编解码和网络传输；图像码流的逐渐呈现便于用户上网检索感兴趣的图像。
    SPIHT算法对图像信息采用如下的编码步骤。
　　首先，定义三个队列：不显著性系数队列LIP，显著性系数队列LSP和不显著性集合队列LIS。
　　设，O（i，j）表示节点（i，j）的直接节点的集合；D（i，j）表示节点（i，j）的子节点集合；L（i，j）表示子节点中排除直接节点后的集合。
　　在队列中，每个元素由一个坐标唯一识别，它在LIP和LSP中代表孤立系数（无子节点的根节点），在LIS中代表第一类元素的D（i，j）或者第二类元素的L（i，j）。
　　对某个阈值T进行显著性测试。将大于T的元素移入LSP，并在LIP队列中移除该元素。对LIS也进行同样的测试，将显著的元素移入LSP，其他的再进行树的分裂。

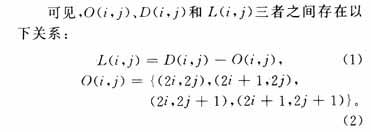
    用类C＋＋语言描述的SPIHT算法如下：
　　第一步，阈值T和三个队列（LSP、LIS和LIP）初始化。

的坐标；


　　（2）if（x，y）是第二类元素，对L（i，j）进行显著性测试
　　if（L（i，j））＝＝1 all（k，l）∈O（i，j）作为第一类元素移入LIS，从LIS出队。
　　第三步，比特传输／存储。将LSP中的每个系数转化成二进制传输／存储。
　　第四步，阈值更新并转至第二步：T／＝2；gotostep2。
3　提升方案与第二代小波
　　提升方法构造小波分为分裂、预测和更新三个步骤。
3．1　分裂（split）
　　将一原始信号序列Sj按偶数和奇数序号分成两个较小的、互不相交的小波子集Sj－1和dj－1：
  
3．2　预测（predict）
　　由于数据间存在相关性，因而可以定义一个预测算子P，使dj－1＝P（Sj－1），这样可用相邻的偶数序列来预测奇数序列。若用dj－1与P（Sj－1）的差值代替dj－1，则其数据量要比原始dj－1小得多。

　　最简单的情况下，取两个相邻偶数序号所在数据的均值作为它们间奇数序号所在数据的预测值。即，

3．3　更新（update）
　　由于上述两个过程一般不能保持原图像中的某些整体性质（如亮度），为此，我们要构造一个U算子去更新Sj－1，使之保持原有数据集的某些特性。

4　编／解码方案
　　本文中前端采用第二代小波（lifTIng wavelet），接着对小波系数采用SPIHT算法，然后，采用Amir Said的自适应算术编码。解码是编码的逆过程，包括与正向SPIHT对应的三个步骤：恢复更新、恢复预测和合并（merge）。编／解码方案如图1所示。

>