基于台达20PM运动控制器的渐开线数控弯管
1 引言
管材塑性加工是以管材作毛坯,通过塑性加工手段,制造管材零件的加工技术 。管材塑性加工由于容易满足塑性成形产品轻量化、强韧化和低耗高效、精确制造等方面的要求,已成为先进塑性加工技术面向21 世纪研究与发展的一个重要方向。
2 数控弯管
2.1 弯管工艺
实践中有许多不同的弯管工艺,从不同的角度出发可以有多种不同的分类。工程中通常按弯曲时加热与否可分为冷弯和热弯,根据弯曲时有无填充物可分为有芯弯管和无芯弯管。 无模弯曲成形是指管材弯曲变形区不直接受到模具的作用,最终的形状由工具和工件的相对运动决定,属于高度灵活的柔性加工手段。有模弯曲成形是指通过刚性模具直接作用于弯曲变形区而进行的管材弯曲,要求此刚性模具作用部分尺寸可以补偿制件卸载后发生的弯曲回弹,属于可重复性高而且快速的加工手段。管材弯曲的几种新工艺包括热应力弯曲;基于工具运动控制的无模弯曲;叠加法弯曲;数控机床绕弯等等。
2.2 数控弯管
数控弯管将管材夹紧在弯曲模上,随弯曲模一起转动,当管材被拉过压块时,压块即将管材绕弯在弯曲管上,属于成形模弯曲工艺。传统绕弯工艺多是手工绕弯,效率低,质量难以保证。随着数控机床业的发展,采用先进的数控弯管机床实现绕弯工艺,可以大大地提高生产效率,保证产品的质量。由于可以方便地调节工艺参数,因此数控弯管机可以既准确又稳定地完成弯曲、送进、转角等动作,保证了管制件的弯曲准确度。数控弯管机可以自动连续地成形不同曲率半径的空间弯曲件。结合相应的数据库软件系统,控制程序还可以预先修正弯曲回弹量。但是该工艺的模具结构(见图7) 比较复杂,制件质量对工艺参数敏感,要求有充分的前期准备和试制工作。尤其是对于弯制薄壁管制件的情况,如果工艺参数选择不当,则很容易出现起皱现象导致零件甚至是模具的报废。如何高效准确地获取这些工艺参数,充分保证弯管产品质量,是数控绕弯工艺的研究热点。
3 数控弯管系统
3.1系统组成
基于台达机电一体化平台的数控弯管设备共有六个运动轴系,工艺要求其中两轴需要直线插补,两轴需要圆弧插补,其它两轴没有特别的要求。PLC控制器选择的是32EH00T2和20PM00D,显示部分选择的是10.4寸触摸屏DOP-AE10THTD1,如表1所示。
表1 数控弯管系统配置
|
名称 |
型号 |
数量 |
|
触摸屏人机界面 |
DOP-AE10THTD1 |
1 |
|
PLC |
DVP-32EH00T2 |
1 |
|
运动控制器 |
DVP-20PM00D |
1 |
|
伺服驱动 |
三菱 |
6 |
3.2 20PM运动控制器
弯管控制系统核心由台达运动控制器DVP-20PMMOOD构成。台达DVP-20PM00D是一款具有运动控制专用功能的可编程控制器。DVP-20PM00D的最大特点是PLC主机直接提供电子凸轮功能,或者说DVP-20PM00D是内置电子凸轮功能的PLC,所以有些场所直接称呼DVP-20PM00D为台达20PM运动控制器。20PM具有2路500KHz的输入与输出,在电子凸轮功能中定义X轴为从轴,编码器输入轴为主轴,当定义好CAM Table后,从轴依据定义的曲线跟随主轴运动。采用高速双CPU结构形式,利用独立CPU处理运动控制算法,可以很好地实现各种运动轨迹控制、逻辑动作控制,直线/圆弧插补控制等,数控弯管机正是利用了20PM运动控制器的电子凸轮功能解决复杂运动轨迹控制问题。
4 20PM数控弯管编程设计
4.1 弯模模式
根据弯管加工要求,开发了两个弯管工艺模式,参见图1所示。
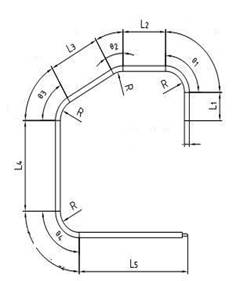
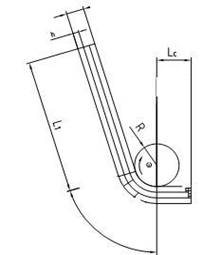
弯模A模式 弯模B模式
图1 弯管模式
4.2 工艺流程
设备分手动和自动模式,手动模式下主要是包括设备回原点、悬臂定长前进/后退、悬臂定长上升/下降以及弯短管时的手动弯模。
设备的自动流程分A模式和B模式,分别对应下面的A流程和B流程,流程之间的切换通过人机来完成。在具体实施中,PLC为主控制器,用来控制流程的选择和跳转等,同时通过PLC给PM命令,以完成PM所担负的工作。
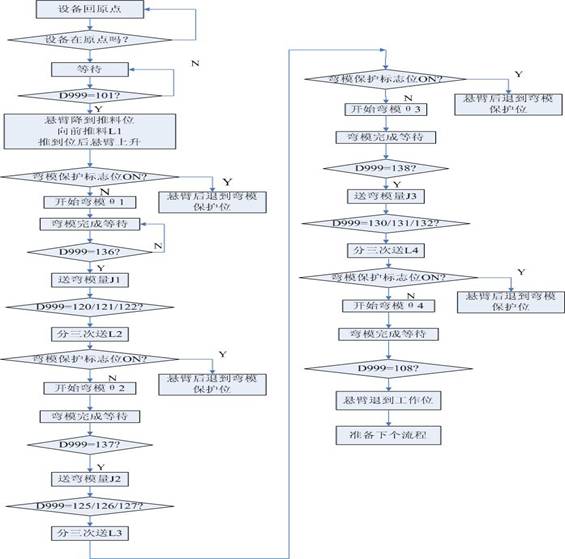
图2 弯模A模式流程图
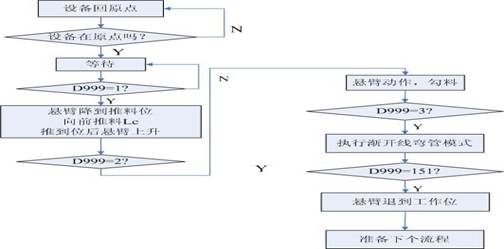
图3 弯模B模式流程图
4.3 渐开线坐标计算
由于20PM自身不支持渐开线方式的插补功能,所以在具体实施中,将渐开线按照弯曲的角度分成多点,通过人机计算出每点的坐标,最后PM通过做直线插补来实现用户要求的功能。当时给出的具体渐开线方程:
X=(R+H)*sinα+(L-α*R)*cosα
Y= R-(R+H)* cosα+(L-α*R)*sinα
其中L,R,H都为常量,可以通过人机设定
在计算时,为了预防编写的宏指令对人机的执行速度造成影响,通过画面cycle宏来实现坐标的计算,这样就不会影响到人机其它页面的操作速度。下面是编写的宏指令:BMOV($88, (2@D664), 2)
BMOV($90, (2@D144), 2)
## X=(R+H)*SINθ+(L-R*θ)COSθ
## Y=R-(R+H)*COSθ+(L-R*θ)SINθ
#初始化运算
IF $58 <= $M56 (Signed DW)
$112 = SIN($58) (Signed DW)
$116 = COS($58) (Signed DW)
$66 = FCNV($58) (Signed DW)
$60 = FCNV($M50) (Signed DW)
$62 = FCNV($M52) (Signed DW)
$64 = FCNV($M54) (Signed DW)
$120 = FDIV($66, 180.0) (Signed DW)
$124 = FMUL($120, 3.14) (Signed DW)
$128 = FMUL($124, $62) (Signed DW)
##R+H
$108 = FADD($62, $64) (Signed DW)
##L-R*θ
$132 = FSUB($60, $128) (Signed DW)
##(R+H)*SINθ
$136 = FMUL($108, $112) (Signed DW)
##(L-R*θ)COSθ
$140 = FMUL($132, $116) (Signed DW)
##(R+H)*COSθ
$144 = FMUL($108, $116) (Signed DW)
##(L-R*θ)SINθ
$148 = FMUL($132, $112) (Signed DW)
##开始计算
## X
$152 = FADD($136, $140) (Signed DW)
## Y
$156 = FSUB($62, $144) (Signed DW)
$160 = FADD($156, $148) (Signed DW)
##角度自加一
$58 = $58 + 1 (Signed DW)
##转成整数并存储
$164 = iCNV($152) (Signed DW)
$168 = iCNV($160) (Signed DW)
$170 = $88 - $164 (Signed DW)
$172 = $90 - $168 (Signed DW)
*$200 = $170 (Signed DW)
*$900 = $172 (Signed DW)
$200 = $200 + 2 (DW)
$900 = $900 + 2 (DW)
ELSEIF $58 < 120 (Signed DW)
$58 = $58 + 1 (Signed DW)
*$200 = 400 (Signed DW)
*$900 = 400 (Signed DW)
$200 = $200 + 2 (DW)
$900 = $900 + 2 (DW)
ELSE
##赋值给PM,并重新初始化
BMOV((2@D3000), $500, 240)
BMOV((2@D3600), $1000, 240)
$58 = 0 (DW)
$200 = 500 (DW)
$900 = 1000 (DW)
SETB $50.0
endif
end
5 结束语
台达PM20运动控制器在执行圆弧插补以及执行连续性的动作流程方面更接近于专业数控系统,有着PLC所不能比拟的优势,尽管在执行程序流程的灵活性方面,和PLC还是有一定的距离。
用管材制造的弯曲零件,无论是平面弯曲件,还是空间弯曲件,除大量应用于气体、液体的输送管路外,在金属结构中的应用也十分广泛。因此管材弯曲成形工艺是备受关注并得到迅速发展的重要领域,开展这方面的研究工作,具有十分重要的意义。