在图像处理系统中常需要对图像进行预处理。由于图像处理的数据量大，对于实时性要求高的系统， 采用软件实现通常难以满足实时性的要求。Altera的QuartusⅡ作为一种可编程逻辑的设计环境，由于其强大的设计能力和直观易用的接口，越来越受 到数字系统设计者的欢迎。QuartusⅡ支持Altera的IP核，包含了LPM／Megafunctions宏功能模块库，设计者只需要选取设置这些 功能模块的相关参数就可以在程序中调用，从而使用户可以充分利用成熟的模块，大大简化了设计的复杂性，加快了设计速度。

拉普拉斯算子是一种重要的图像增强算子，它是一种各向同性滤波器，即滤波器的响应与滤波器作用图像的突变方向无关，而且实现简单，被广泛用于图像锐化和高频增强等算法中。在此，提出一种使用QuartusⅡ开发环境的Megafunctions功能模块实现拉普拉斯算子的方案，可以做到实时增强图像的高频细节。

1 、Laplacian算子介绍拉普拉斯算子是各向同性线性算子，二元函数f（x，y）的拉普拉斯变换定义为：

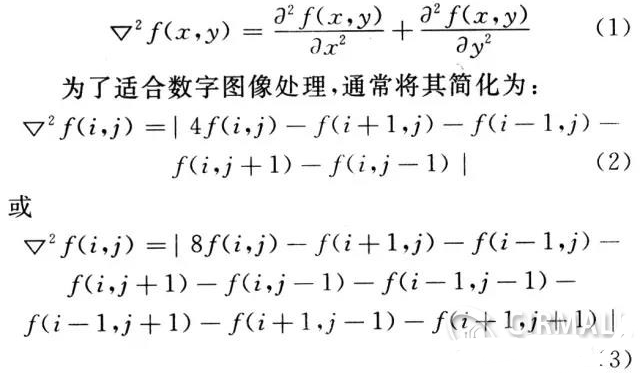
基本高通滤波模板中所有系数的和为0，如果在模板所覆盖的区域内像素的灰度值都相同或者灰度值的变化较为缓慢．则模板的输出为0或输出很小。人们常用的高通提升滤波方法，就是将原图像乘以一个放大因子A，再减去低通滤波图像。高通提升滤波可以表示为： 高通提升滤波图像=A×原图像-低通滤波图像=（A-1）×原图像+原图像-低通滤波图像=（A-1）×原图像+高通滤波图像

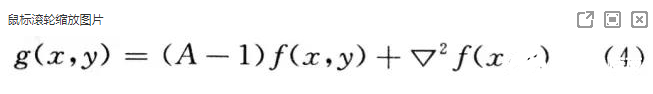
即：

式中：当A=1时，高通提升滤波就是基本的高通滤波；当A》1时，部分原图像被加到高通滤波的结果上，这就恢复了部分高通滤波中丢失的低频成分。因此，经过高通提升滤波的图像与原图像更加相像，同时又对图像的边缘进行了增强。进行模板卷积的主要步骤为：

（1）将模板在图中漫游，并将模板中心与图中某个像素位置重合；

（2）将模板上系数与模板下对应像素相乘；

（3）将所有乘积相加；

（4）将和（模板的输出响应）赋给图中对应模板中心位置的像素。当模板遍历图像中的每个像素就得到图像滤波结果。实现Laplacian高通提升滤波的模板如图1所示。

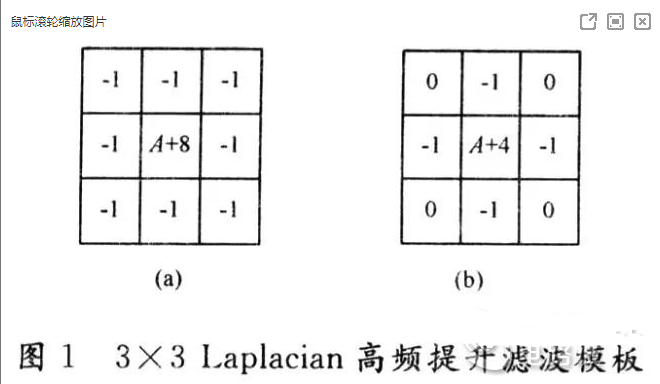
文献［2］的实验证明，使用图1（a）所示掩模能得到更好的锐化效果，所以在硬件实现时使用该掩模。实验中取A=1。